https://www.acmicpc.net/problem/2133
2133번: 타일 채우기
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
www.acmicpc.net

문제
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
입력
첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.
출력
첫째 줄에 경우의 수를 출력한다.
예제 입력 1 복사
2
예제 출력 1 복사
3
힌트
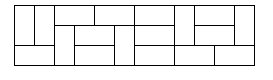
아래 그림은 3×12 벽을 타일로 채운 예시이다.
내 풀이
전에 이와 비슷한 문제를 풀어본 기억이 있어서 별로 어렵지 않을 것이라고 생각하고 접근하였다.
처음에 답을 냈을 때, '엥 이게 왜 골드4지?' 라는 생각이 들었었고 답을 제출했지만 당연히 틀려버렸다.
그 후 생각을 거듭한 결과, 단순하게 풀 수 있는 문제가 아니라는 것을 깨닫고 생각을 거듭하면 거듭할수록
간단하게 풀 수 있는 dp문제가 아니란 것을 깨달았다.
풀이를 설명하자면
1. N이 홀수면 타일을 채울 수 없다.
-> 타일 갯수가 홀수인데 짝수개의 벽돌로 채울 수 없다.
N이 홀수면 dp[N] = 0
2. N이 짝수일 때, dp로는 해결할 수 없는 특이한 모양의 타일이 존재한다.
ex) N = 4 일때,
ex) N = 6 일때,
내가 풀 알고리즘의 전략은 i번째 타일을 칠하는 방법의 수는 i-2번째 타일을 칠하는 방법의 수로 조작하는 거였는데,
i-2번째 타일과 관련이 없는 방법의 수가 항상 2가지 씩 나온다.
dp[i] += 2
3. (i번째 타일을 칠하는 방법의 수) = (i-2번째 타일을 칠하는 방법의 수) * 3
3*2 타일을 칠하는 방법의 수는 총 3가지가 존재하므로
dp[i] = dp[i-2] * 3
4. (i번째 타일을 칠하는 방법의 수) = (i-j 번째 타일을 칠하는 방법의 수) * 2
아까 2번에서 말했던 특이한 모양의 타일이 항상 존재하므로
j가 4이상의 짝수일때,
dp[i] = dp[i-j] * 2
따라서 이를 모두 다 더하면 답이 된다!
코드
# 타일채우기
import sys
input = sys.stdin.readline
N = int(input())
if N == 1:
print(0)
exit()
dp = [0 for _ in range(N+1)]
dp[2] = 3
for i in range(4, N+1, 2):
for j in range(2, i, 2):
count = 2
if j == 2:
count = 3
dp[i] += dp[i-j]*count
dp[i] += 2
print(dp[N])
'Algorithm > Python' 카테고리의 다른 글
| [BOJ] 1562번 : 계단 수 [G1] (0) | 2023.07.27 |
|---|---|
| [파이썬] List, Tuple, Set, Dictionary (0) | 2023.07.05 |
| [BOJ] 5430번 : AC [G5] (0) | 2023.02.12 |


